概念
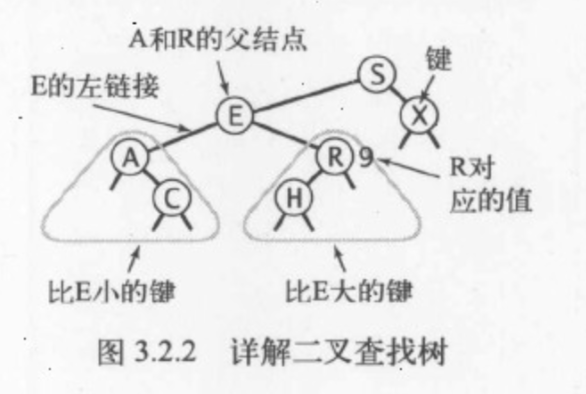
二叉查找树是一种能够将链表插入的灵活性,以及有序数组查找的高效结合起来的符号表实现。二叉查找树中,每个节点包含两个链接(链表中每个节点只包含一个链接),分别指向自己的左子节点以及右子节点,每个节点的键都大于自己的左子树中的任意键而小于右子树中的任意键。可以理解为,每一个链接指向另一颗子二叉树。
API
图解
代码实现
基于链表
1 | public class BST<K extends Comparable<K>, V> { |
参考文档
《算法》
二叉查找树是一种能够将链表插入的灵活性,以及有序数组查找的高效结合起来的符号表实现。二叉查找树中,每个节点包含两个链接(链表中每个节点只包含一个链接),分别指向自己的左子节点以及右子节点,每个节点的键都大于自己的左子树中的任意键而小于右子树中的任意键。可以理解为,每一个链接指向另一颗子二叉树。

基于链表
1 | public class BST<K extends Comparable<K>, V> { |
《算法》