算法练习_基于线性探测法的散列表

Posted on | Comments: | Views:
散列表的学习笔记以及代码实现

概念

散列表（哈希表）是一种无序符号表，将键作为数组的索引，而数组中键 i 处就是它对应的值，这样可以增大访问速度。散列算法分为两步：

  • 用散列函数将键转化为一个索引
  • 处理碰撞冲突（理想情况下，散列函数会将不同的键转化为不同的散列值，但在实际情况中，我们需要面对不同的键散列到相同索引的情况。）

基于线性探测法的散列表

线性探测法的实现方式用大小为 M 的并行数组保存 N 个键值对（M>N），一条保存键，一条保存值，使用散列函数产生访问数组的索引，依靠数组中的空位解决碰撞冲突。
线性探测的查找做法是：当发生碰撞时，直接检查散列表中的下一个位置；如果下一个位置不为空，且与被查找的键不相同，则继续下一个查找；如果命中，则返回当前值。直到遇到一个空元素。这些空元素可以作为查找结束的标志。

删除操作

线性探测法的删除操作较为复杂，因为无法直接将该位置的键和值设置为 null ;这会导致后续键值对无法访问。因此，当执行删除操作时，需要将删除的键值对，其右的所有键值对重新插入散列表。

重置数组大小

线性探测的平均成本取决于元素在插入数组后聚集成的一组连续的条目，称为键簇。随着插入的键越来越多，较长的键簇也会越来越多。这时，为了保证效率，需要调整数组大小。通常，散列表的使用率 （N/M）保持在 1/8 到 1/2 之间（注意：不允许散列表被沾满，否则未命中的查找会导致无限循环）。

图解

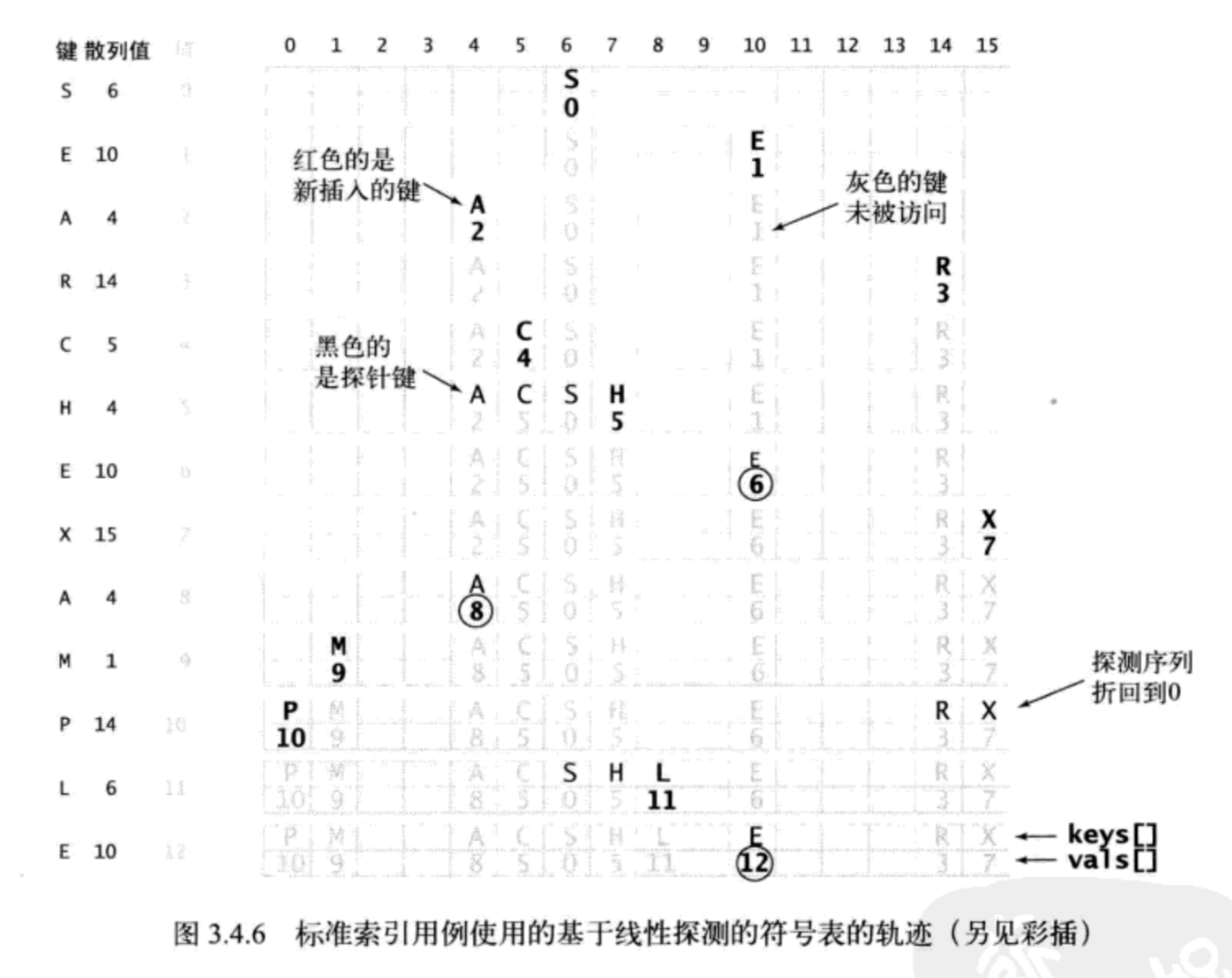
F6pefO.png

代码实现

基于线性探测法的散列表：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
public class LinearProbingHashST<K, V> {

    int M;
    int N;
    K[] keys;
    V[] values;

    public LinearProbingHashST(int cap) {
        M = cap;
        N = 0;
        this.keys = (K[]) new Object[M];
        this.values = (V[]) new Object[M];
    }

    int hash(K key) {
        return (key.hashCode() & 0x7fffffff) % M;
    }

    void put(K key, V value) {
        if (N > M / 2) {
            resize(M * 2);
        }
        int i;
        for (i = hash(key); keys[i] != null; i = (i + 1) % M) {
            if (keys[i].equals(key)) {
                values[i] = value;
                return;
            }
        }
        keys[i] = key;
        values[i] = value;
        N++;
    }

    V get(K key) {
        if (key == null) {
            return null;
        }
        int i;
        for (i = hash(key); keys[i] != null; i = (i + 1) % M) {
            if (keys[i].equals(key)) {
                return values[i];
            }
        }
        return null;
    }

    void delete(K key) {
        if (key == null) {
            return;
        }
        if (!contains(key)) {
            return;
        }

        int i = hash(key);
        while (!keys[i].equals(key)) {
            i = (i + 1) % M;
        }

        keys[i] = null;
        values[i] = null;
        N--;

        i++;
        while (keys[i] != null) {
            K newK = keys[i];
            V newV = values[i];
            keys[i] = null;
            values[i] = null;
            N--;
            put(newK, newV);
            i = (i + 1) % M;
        }

        if (N > 0 && N < M / 8) {
            resize(M / 2);
        }
    }

    boolean contains(K key) {
        if (key == null) {
            return false;
        }

        int i;
        for (i = hash(key); keys[i] != null; i = (i + 1) % M) {
            if (keys[i].equals(key)) {
                return true;
            }
        }
        return false;
    }

    void resize(int cap) {
        LinearProbingHashST<K, V> st = new LinearProbingHashST<>(cap);
        for (int i = 0; i < M; i++) {
            if (keys[i] != null) {
                st.put(keys[i], values[i]);
            }
        }
        keys = st.keys;
        values = st.values;
        M = st.M;
    }
}